9. Markov Chain Monte Carlo
Contents
9. Markov Chain Monte Carlo¶
# Install packages that are not installed in colab
try:
import google.colab
%pip install -q watermark
%pip install git+https://github.com/ksachdeva/rethinking-tensorflow-probability.git
except:
pass
%load_ext watermark
from functools import partial
from jax import ops
import jax.numpy as jnp
# Core
import numpy as np
import arviz as az
import pandas as pd
import tensorflow as tf
import tensorflow_probability as tfp
# visualization
import matplotlib.pyplot as plt
from rethinking.data import RethinkingDataset
from rethinking.data import dataframe_to_tensors
from rethinking.mcmc import sample_posterior
# aliases
tfd = tfp.distributions
Root = tfd.JointDistributionCoroutine.Root
2022-01-19 19:01:51.571884: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcudart.so.11.0'; dlerror: libcudart.so.11.0: cannot open shared object file: No such file or directory
%watermark -p numpy,tensorflow,tensorflow_probability,arviz,scipy,pandas,rethinking
numpy : 1.21.5
tensorflow : 2.7.0
tensorflow_probability: 0.15.0
arviz : 0.11.4
scipy : 1.7.3
pandas : 1.3.5
rethinking : 0.1.0
# config of various plotting libraries
%config InlineBackend.figure_format = 'retina'
Introduction¶
9.1 Good King Markov and His island kingdom¶
Code 9.1¶
# Takes few minutes to run
num_weeks = int(1e5)
positions = np.repeat(0, num_weeks)
current = 10
coin_dist = tfd.Bernoulli(probs=0.5)
proposal_dist = tfd.Uniform(low=0.0, high=1.0)
for i in range(num_weeks):
# record current position
positions[i] = current
# flip coin to generate proposal
bern = coin_dist.sample().numpy()
proposal = current + (bern * 2 - 1)
# now make sure he loops around the archipelago
proposal = np.where(proposal < 1, 10, proposal)
proposal = np.where(proposal > 10, 1, proposal)
# move?
prob_move = proposal / current
unif = proposal_dist.sample().numpy()
current = np.where(unif < prob_move, proposal, current)
2022-01-19 19:01:53.728325: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcuda.so.1'; dlerror: libcuda.so.1: cannot open shared object file: No such file or directory
2022-01-19 19:01:53.728361: W tensorflow/stream_executor/cuda/cuda_driver.cc:269] failed call to cuInit: UNKNOWN ERROR (303)
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
/tmp/ipykernel_2260/2591419575.py in <module>
23 # move?
24 prob_move = proposal / current
---> 25 unif = proposal_dist.sample().numpy()
26 current = np.where(unif < prob_move, proposal, current)
/opt/hostedtoolcache/Python/3.7.12/x64/lib/python3.7/site-packages/tensorflow_probability/python/distributions/distribution.py in sample(self, sample_shape, seed, name, **kwargs)
1232 """
1233 with self._name_and_control_scope(name):
-> 1234 return self._call_sample_n(sample_shape, seed, **kwargs)
1235
1236 def _call_sample_and_log_prob(self, sample_shape, seed, **kwargs):
/opt/hostedtoolcache/Python/3.7.12/x64/lib/python3.7/site-packages/tensorflow_probability/python/distributions/distribution.py in _call_sample_n(self, sample_shape, seed, **kwargs)
1210 sample_shape, 'sample_shape')
1211 samples = self._sample_n(
-> 1212 n, seed=seed() if callable(seed) else seed, **kwargs)
1213 samples = tf.nest.map_structure(
1214 lambda x: tf.reshape(x, ps.concat([sample_shape, ps.shape(x)[1:]], 0)),
/opt/hostedtoolcache/Python/3.7.12/x64/lib/python3.7/site-packages/tensorflow_probability/python/distributions/uniform.py in _sample_n(self, n, seed)
154 shape = ps.concat([[n], self._batch_shape_tensor(
155 low=low, high=high)], 0)
--> 156 samples = samplers.uniform(shape=shape, dtype=self.dtype, seed=seed)
157 return low + self._range(low=low, high=high) * samples
158
/opt/hostedtoolcache/Python/3.7.12/x64/lib/python3.7/site-packages/tensorflow_probability/python/internal/samplers.py in uniform(shape, minval, maxval, dtype, seed, name)
282 seed = sanitize_seed(seed)
283 return tf.random.stateless_uniform(
--> 284 shape=shape, seed=seed, minval=minval, maxval=maxval, dtype=dtype)
/opt/hostedtoolcache/Python/3.7.12/x64/lib/python3.7/site-packages/tensorflow/python/util/traceback_utils.py in error_handler(*args, **kwargs)
148 filtered_tb = None
149 try:
--> 150 return fn(*args, **kwargs)
151 except Exception as e:
152 filtered_tb = _process_traceback_frames(e.__traceback__)
/opt/hostedtoolcache/Python/3.7.12/x64/lib/python3.7/site-packages/tensorflow/python/util/dispatch.py in op_dispatch_handler(*args, **kwargs)
1094 # Fallback dispatch system (dispatch v1):
1095 try:
-> 1096 return dispatch_target(*args, **kwargs)
1097 except (TypeError, ValueError):
1098 # Note: convert_to_eager_tensor currently raises a ValueError, not a
/opt/hostedtoolcache/Python/3.7.12/x64/lib/python3.7/site-packages/tensorflow/python/ops/stateless_random_ops.py in stateless_random_uniform(shape, seed, minval, maxval, dtype, name, alg)
342 with ops.name_scope(name, "stateless_random_uniform",
343 [shape, seed, minval, maxval]) as name:
--> 344 shape = tensor_util.shape_tensor(shape)
345 if dtype.is_integer and minval is None:
346 key, counter, alg = _get_key_counter_alg(seed, alg)
/opt/hostedtoolcache/Python/3.7.12/x64/lib/python3.7/site-packages/tensorflow/python/framework/tensor_util.py in shape_tensor(shape)
1081 # not convertible to Tensors because of mixed content.
1082 shape = tuple(map(tensor_shape.dimension_value, shape))
-> 1083 return ops.convert_to_tensor(shape, dtype=dtype, name="shape")
1084
1085
/opt/hostedtoolcache/Python/3.7.12/x64/lib/python3.7/site-packages/tensorflow/python/profiler/trace.py in wrapped(*args, **kwargs)
161 with Trace(trace_name, **trace_kwargs):
162 return func(*args, **kwargs)
--> 163 return func(*args, **kwargs)
164
165 return wrapped
/opt/hostedtoolcache/Python/3.7.12/x64/lib/python3.7/site-packages/tensorflow/python/framework/ops.py in convert_to_tensor(value, dtype, name, as_ref, preferred_dtype, dtype_hint, ctx, accepted_result_types)
1584 if dtype is not None:
1585 dtype = dtypes.as_dtype(dtype)
-> 1586 if isinstance(value, Tensor):
1587 if dtype is not None and not dtype.is_compatible_with(value.dtype):
1588 raise ValueError(
KeyboardInterrupt:
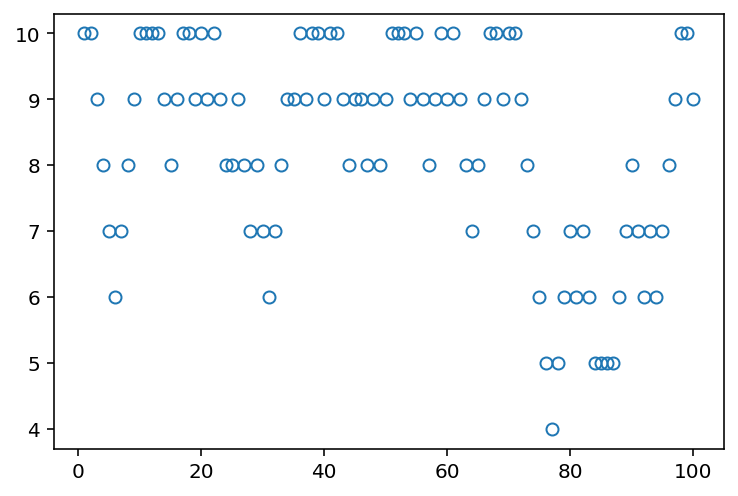
Code 9.2¶
plt.plot(range(1, 101), positions[:100], "o", mfc="none");
[<matplotlib.lines.Line2D at 0x14b8e3b10>]
Code 9.3¶
plt.hist(positions, bins=range(1, 12), rwidth=0.1, align="left");
(array([ 1877., 3575., 5267., 7174., 9175., 11077., 12910., 14408.,
16217., 18320.]),
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]),
<BarContainer object of 10 artists>)
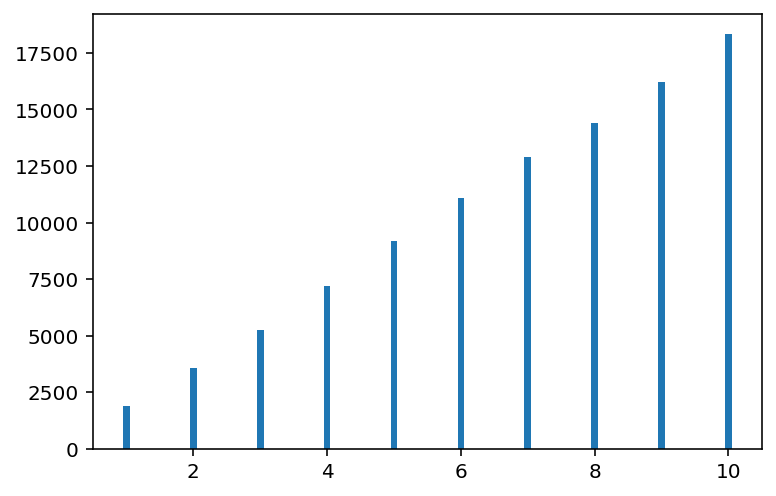
In above plot, horizontal axis is the islands (and their relative populations). Vertical axis is the number of weeks that King stayed at that island
9.2 Metropolis Algorithms¶
9.2.1 Gibbs sampling¶
9.2.2 High-dimensional problems¶
Code 9.4¶
What this section demonstrates is that as the number of dimensions increase the mass of the samples move away from the peak.
T = int(1e3)
_, ax = plt.subplots(2, 2, figsize=(8, 4))
plt.xlabel("Radial distance from the mode")
def build_and_plot(d, ax_p):
loc = tf.cast(np.repeat(0, d), dtype=tf.float32)
scale_diag = np.identity(d, dtype=np.float32)
Y = tfd.MultivariateNormalDiag(loc=loc, scale_diag=scale_diag).sample((T,)).numpy()
rad_dist = lambda Y: np.sqrt(np.sum(Y ** 2))
Rd = list(map(lambda i: rad_dist(Y[i]), np.arange(T)))
az.plot_kde(np.array(Rd), bw=0.18, label=f"Dim = {d}", ax=ax_p)
build_and_plot(1, ax[0][0])
build_and_plot(10, ax[0][1])
build_and_plot(100, ax[1][0])
build_and_plot(1000, ax[1][1])
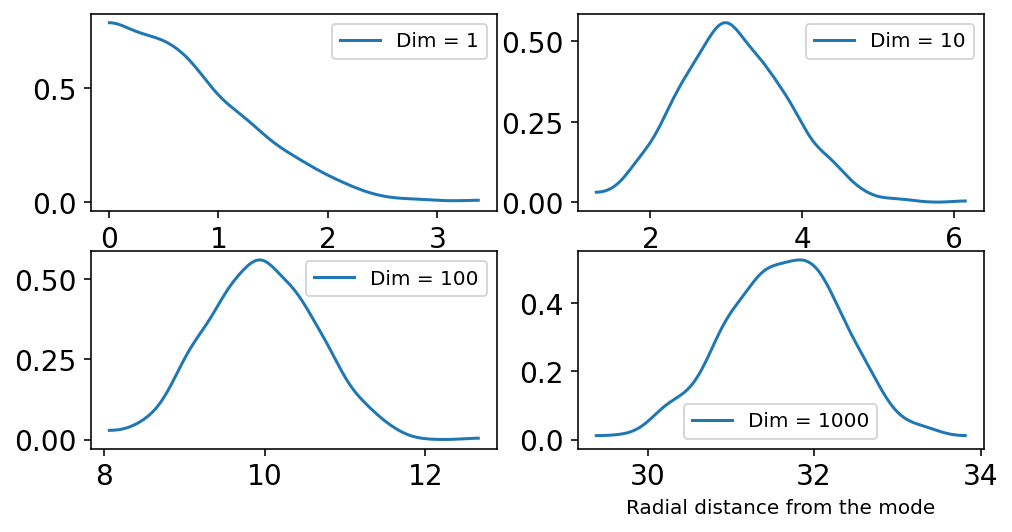
In the above plot, the horizontal axis shows Radial distance from the mode in the parameter space.
The peak in the above diagrams represent the amount of samples.
For Dim == 1, the peak is near 0
For Dim == 10, the peak is far from zero already
and so on …
The sampled points are in a thin, high-dimensional shell very far from the mode.
Because of above behavior (i.e. high dimensionsal space), the author suggests we need better MCMC algos than Metropolios and Gibbs
9.3 Hamiltonian Monte Carlo¶
Code 9.5¶
These next few cells will implement the Hamiltonian Monte Carlo algo. (Overthinking box in the chapter)
We need five things to do that -
A function named
Uthat returns the -ive log-prob of data at a current position (parameter value)A function named
grad_Uthat returns the gradient of the -ive log-prob at the current positionA step size
epsilonA count of leapfrog steps
LA starting position
current_q
Note - The position is a vector of parameter values & that the gradient also needs to return the vector of the same lenght.
## Note - change from the book here
#
# The book generates the test data in code 9.6 but I am going to generate it here
def generate_test_data():
# test data
_SEED = 7
seed = tfp.util.SeedStream(seed=_SEED, salt="Testdata")
y = tfd.Normal(loc=0.0, scale=1.0).sample(50, seed=seed()).numpy()
x = tfd.Normal(loc=0.0, scale=1.0).sample(50, seed=seed()).numpy()
# standardize the data
y = (y - np.mean(y)) / np.std(y)
x = (x - np.mean(x)) / np.std(x)
return x, y
x, y = generate_test_data()
y
array([ 0.12833239, -0.22964787, -0.40774608, -0.30924067, -0.75710726,
-1.12151 , 0.54429084, 0.20373885, 0.5373924 , 2.2354805 ,
-0.55821157, 0.8479281 , -0.01069919, -2.2879438 , 2.1183472 ,
0.5721366 , 1.5381907 , -2.4450817 , -0.15067661, 0.0314163 ,
-0.06329995, -1.5469027 , 0.6112922 , -0.6234371 , 0.7724736 ,
0.31413972, 2.2127857 , -0.30521753, -0.06263847, 0.60814875,
1.7873812 , -0.23929906, -0.1567227 , -0.09433585, -0.25074163,
0.3817731 , -1.289493 , -0.03346271, -0.25672948, -0.02745551,
1.6410016 , -1.2717627 , -0.18327089, 0.6673328 , -0.7348228 ,
-0.5346852 , -1.177903 , -0.9149043 , -0.3239217 , 0.6152883 ],
dtype=float32)
def U(q, a=0.0, b=1.0, k=0.0, d=1.0):
muy = q[0]
mux = q[1]
logprob_y = tf.reduce_sum(tfd.Normal(loc=muy, scale=1.0).log_prob(y)).numpy()
logprob_x = tf.reduce_sum(tfd.Normal(loc=mux, scale=1.0).log_prob(x)).numpy()
logprob_muy = tfd.Normal(loc=a, scale=b).log_prob(muy).numpy()
logprob_mux = tfd.Normal(loc=k, scale=d).log_prob(mux).numpy()
return -(logprob_y + logprob_x + logprob_muy + logprob_mux)
Code 9.6¶
def U_gradient(q, a=0.0, b=1.0, k=0.0, d=1.0):
muy = q[0]
mux = q[1]
G1 = np.sum(y - muy) + (a - muy) / b ** 2 # dU/dmuy
G2 = np.sum(x - mux) + (k - mux) / b ** 2 # dU/dmux
return np.stack([-G1, -G2]) # negative bc energy is neg-log-prob
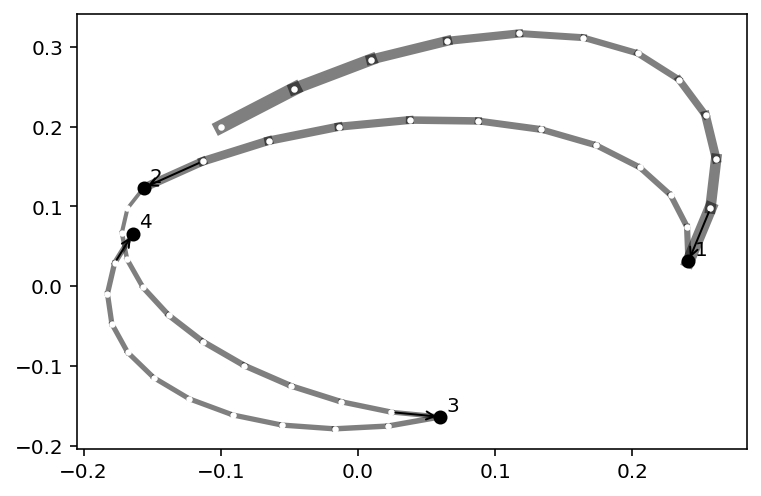
Code 9.7, 9.8, 9.9 & 9.10¶
Q = {}
Q["q"] = np.array([-0.1, 0.2])
pr = 0.31
plt.subplot(ylabel="muy", xlabel="mux", xlim=(-pr, pr), ylim=(-pr, pr))
step = 0.03
L = 11 # 0.03/28 for U-turns --- 11 for working example
n_samples = 4
path_col = (0, 0, 0, 0.5)
for r in 0.075 * np.arange(2, 6):
plt.gca().add_artist(plt.Circle((0, 0), r, alpha=0.2, fill=False))
plt.scatter(Q["q"][0], Q["q"][1], c="k", marker="x", zorder=4)
<matplotlib.collections.PathCollection at 0x14bd51d50>
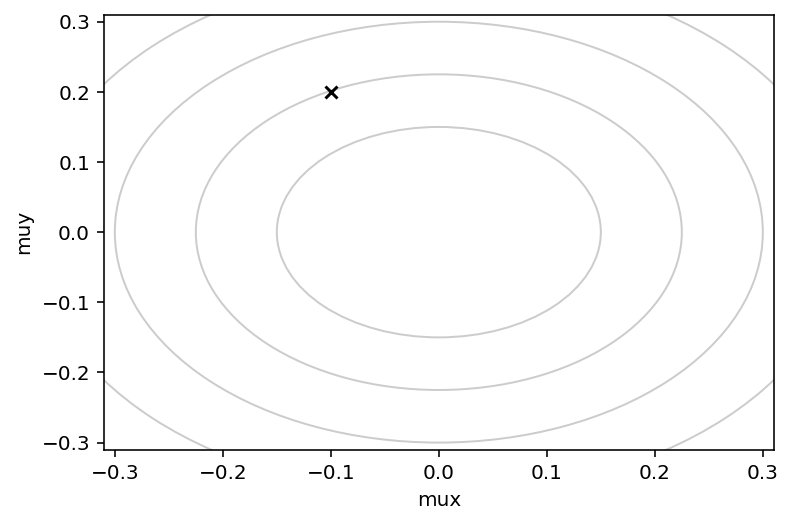
def HMC2(U, grad_U, epsilon, L, current_q):
q = current_q
# Random flick - p is the momentum
p = tfd.Normal(loc=0.0, scale=1.0).sample(q.shape[0]).numpy()
current_p = p
# Make a half step for momentum at the begining
p = p - epsilon * grad_U(q) / 2
# initialize bookkeeping - saves trajectory
qtraj = jnp.full((L + 1, q.shape[0]), np.nan)
ptraj = qtraj
qtraj = ops.index_update(qtraj, 0, current_q)
ptraj = ops.index_update(ptraj, 0, p)
# Alternate full steps for position and momentum
for i in range(L):
q = q + epsilon * p # Full step for the position
# Make a full step for the momentum, except at end of trajectory
if i != (L - 1):
p = p - epsilon * grad_U(q)
ptraj = ops.index_update(ptraj, i + 1, p)
qtraj = ops.index_update(qtraj, i + 1, q)
# Make a half step for momentum at the end
p = p - epsilon * grad_U(q) / 2
# ptraj[L] = p
ptraj = ops.index_update(ptraj, L, p)
# Negate momentum at end of trajectory to make the proposal symmetric
p = -p
# Evaluate potential and kinetic energies at start and end of trajectory
current_U = U(current_q)
current_K = np.sum(current_p ** 2) / 2
proposed_U = U(q)
proposed_K = np.sum(p ** 2) / 2
# Accept or reject the state at end of trajectory, returning either
# the position at the end of the trajectory or the initial position
accept = 0
runif = tfd.Uniform(low=0.0, high=1.0).sample().numpy()
if runif < np.exp(current_U - proposed_U + current_K - proposed_K):
new_q = q # accept
accept = 1
else:
new_q = current_q # reject
return {
"q": new_q,
"traj": qtraj,
"ptraj": ptraj,
"accept": accept,
"dH": proposed_U + proposed_K - (current_U + current_K),
}
for i in range(n_samples):
Q = HMC2(U, U_gradient, step, L, Q["q"])
if n_samples < 10:
for j in range(L):
K0 = np.sum(Q["ptraj"][j] ** 2) / 2
plt.plot(
Q["traj"][j : j + 2, 0],
Q["traj"][j : j + 2, 1],
c=path_col,
lw=1 + 2 * K0,
)
plt.scatter(Q["traj"][:, 0], Q["traj"][:, 1], c="white", s=5, zorder=3)
# for fancy arrows
dx = Q["traj"][L, 0] - Q["traj"][L - 1, 0]
dy = Q["traj"][L, 1] - Q["traj"][L - 1, 1]
d = np.sqrt(dx ** 2 + dy ** 2)
plt.annotate(
"",
(Q["traj"][L - 1, 0], Q["traj"][L - 1, 1]),
(Q["traj"][L, 0], Q["traj"][L, 1]),
arrowprops={"arrowstyle": "<-"},
)
plt.annotate(
str(i + 1),
(Q["traj"][L, 0], Q["traj"][L, 1]),
xytext=(3, 3),
textcoords="offset points",
)
plt.scatter(
Q["traj"][L + 1, 0],
Q["traj"][L + 1, 1],
c=("red" if np.abs(Q["dH"]) > 0.1 else "black"),
zorder=4,
)
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)